科普下搜索索引里常用的压缩算法

2022-01-18

前言

数据压缩是存储领域常用的优化手段，压缩算法可以减少数据的大小减少存储成本、减少磁盘的寻道时间提高I/O的性能、减少数据的传输时间并提高缓冲区的命中率，节省的I/O时间可以轻易补偿它带来的CPU额外开销。目前在用的主流压缩算法包括zlib、snappy和lz4等。压缩算法并不是压缩比越高越好，压缩比越高，其解压缩速度可能越慢，CPU消耗就会越大，这需要根据硬件配置和业务场景做Trade off。本文主要介绍了如下几种搜索索引里常见的压缩算法，大部分压缩算法也适用于OLAP领域，同时有些场景可能需要结合多种场景实现，比如倒排索引的posting list压缩就需要结合PForDelta及Simple算法才能获得更好的压缩比。同时在选择压缩算法时，也会考虑该压缩算法是否支持流式压缩等。

Fixed length
Variable Byte
Improved Variable Byte
Group Varint
Run Length Encoding
Dictionary Coding
Simple 9
Simple 16
PForDelta
Huffman Coding
LZ77
Elasticsearch 行存压缩算法

Fixed length

压缩方法

找到一组数据的最大值，之后计算出最大位宽N：

示例

1	10,35,100,170,370,29000,30000,30010

2^15 = 32768 > 30010，则位宽为15，即每个32bit的数据可以用15bit表示

Variable Byte

压缩方法

每个Byte的第一bit为flag，表示是否继续使用下一个Byte，剩下7位为有效位，所有的有效位组成数字的2进制表示。

示例

1	10,35,100,170,370,29000,30000,30010

10,35,100：这三个数字小于2^7，则三个数字各需要1个Byte
170,370：这两个数字大于2^7，小于2^14，所以各需要2个Byte
29000,30000,30010：这三个数字大于2^14，小于2^21，所以各需要3个Byte
如图所示：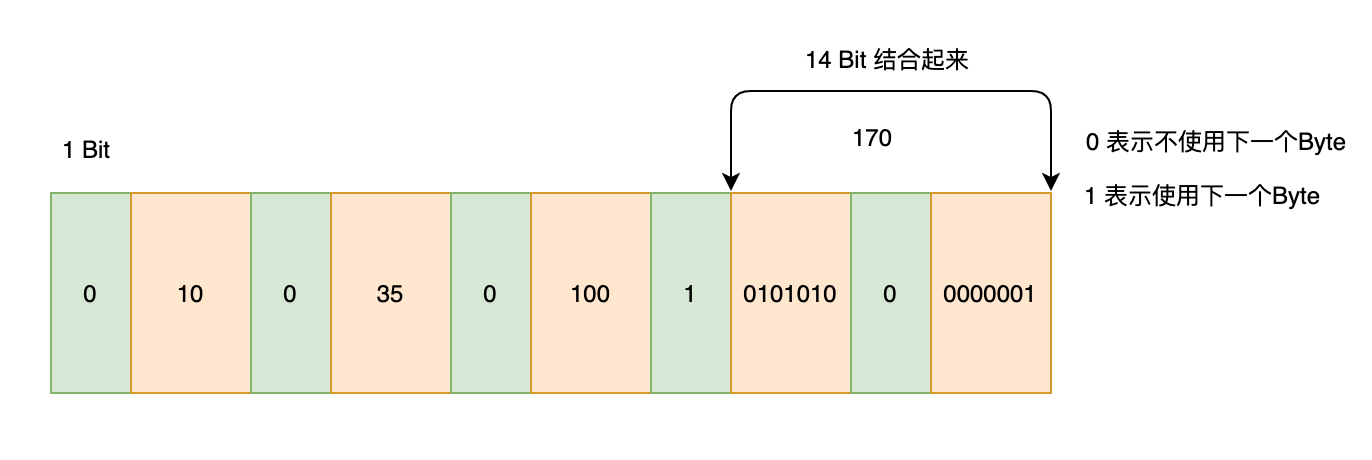

综上：这8个32bit的数字（832）共需要13+22+33 = 16 Byte

Improved Variable Byte

压缩方法

与Variable Byte相似，但是存储的是差值

示例

1	10,35,100,170,370,29000,30000,30100

存储差值后变为：

1	10,25,65,70,200,28630,1000,100

10,25,65,70,100：这五个数字小于2^7，各需要1个Byte表示

200,1000: 这两个数字大于2^7小于2^14，则各需要2个Byte表示

28630: 这个数字大于2^14小于2^21，则需要3个Byte

综上：这8个32bit的数字（832）共需要 51+2*2+3 = 12 Byte

Group Varint

压缩方法

4个数为1组，第一个Byte里面每2个bit记录这个数需要的Byte数，后续4个Byte分别是具体的值。

示例

1	10,25,65,70,200,28630,1000,100

第一组：
10,25,65,70: 第一个Byte里每2bit表示这个数字需要的Byte数，分别为00 00 00 00,以上00表示需要1个Byte，即共需要1+4*1等于5 Byte

如图所示：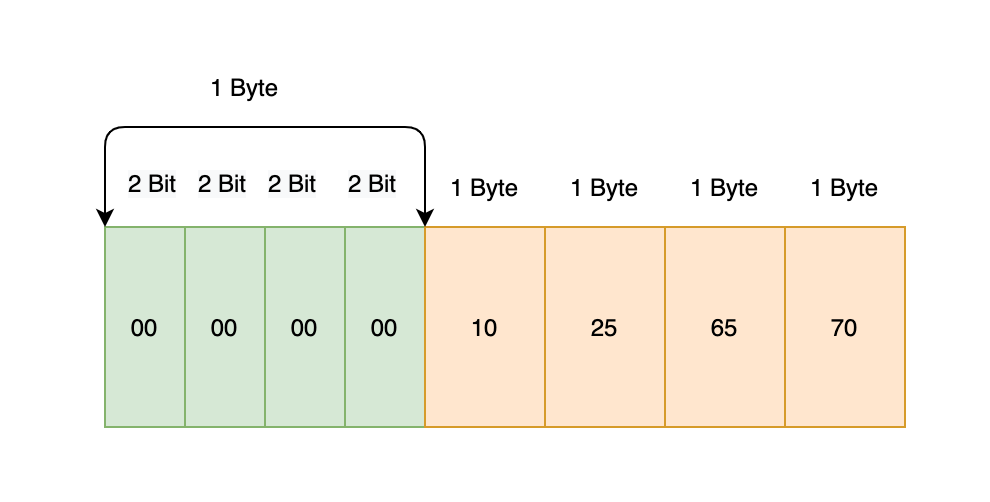

第二组：
200,28630,1000,100: 第一个Byte里每2bit表示这个数字需要的Byte数，分别为00 01 01 00，即共需要1+1+2+2+1 = 7 Byte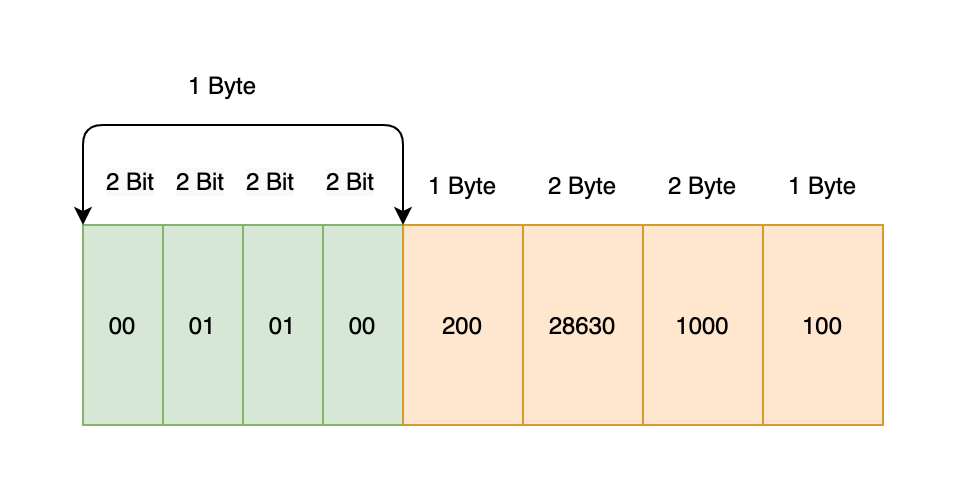

综上：共需要5+7等于12个Byte

Run Length Encoding

压缩方法

RLE：根据字符串的连续重复字符进行编码的一种方法

示例

压缩前：

1	AAAAAABBCDDEEEEEF1

压缩后：

1	A6B2C1D2E5F1

Dictionary Coding

压缩方法

把文本中单词或词汇组合做成一个对应的字典列表，并用特殊代码来表示这个单词或词汇。

示例

字典列表：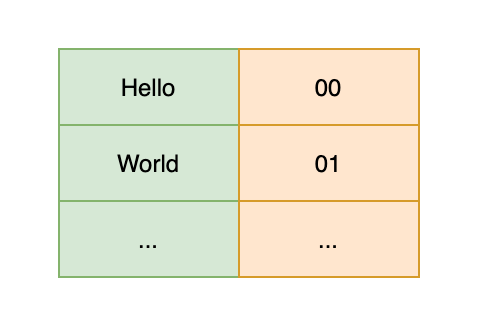

源文本：Hello World，压缩后的编码为：00 01

Simple 9

压缩方法

S9压缩算法，是Simple 系列压缩算法的一员，就是把一个32位的int类型分为两个区域，前四个bit记录后面28bit的使用方式，即模式，后面28位用来存放多个数值，每个数值所占的位数都是等分的，等于28/n，只所以被称为S9，是因为前四个bit表示9 种状态，列表如下:

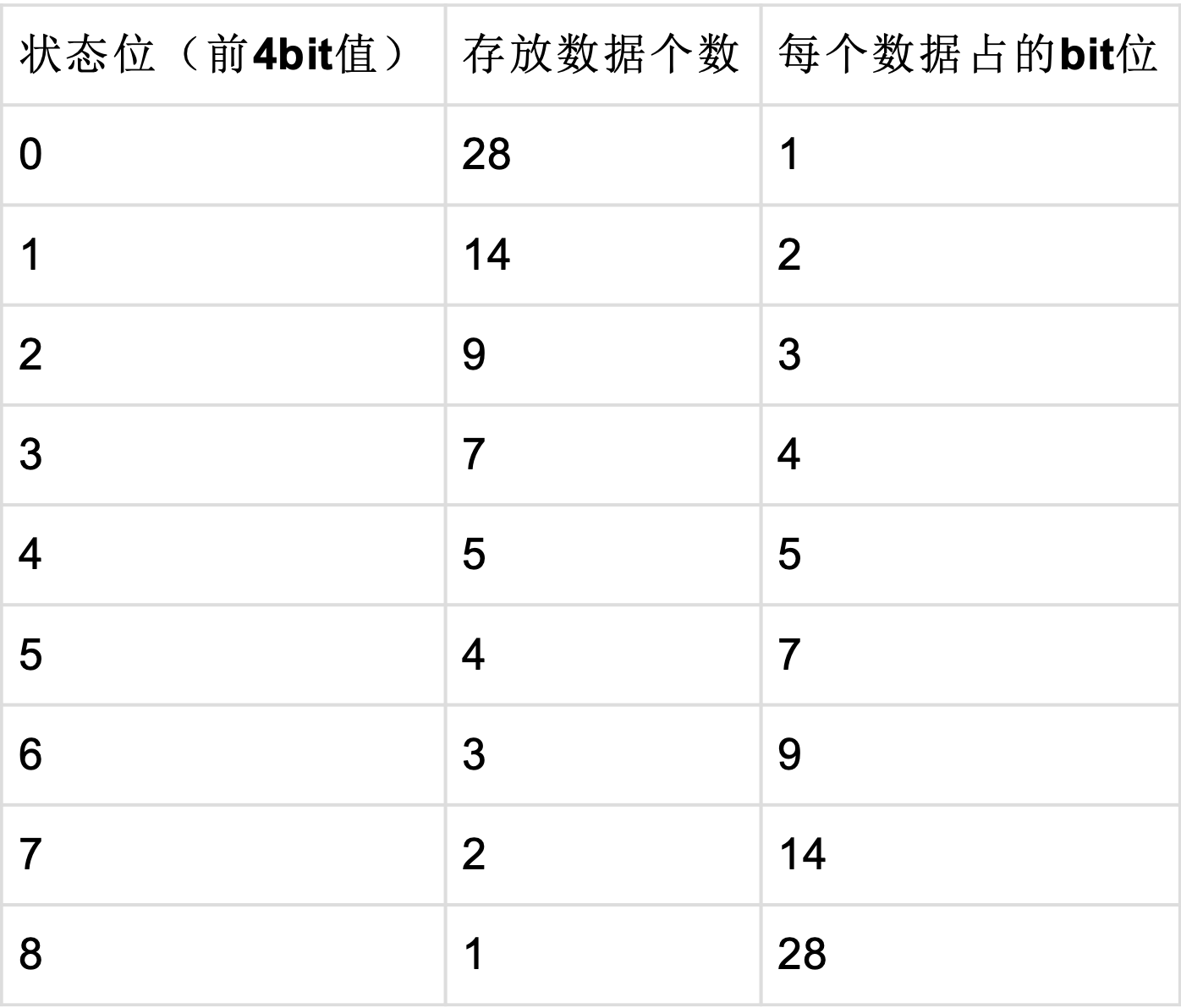
可选择的位宽和对应存储的数据个数:

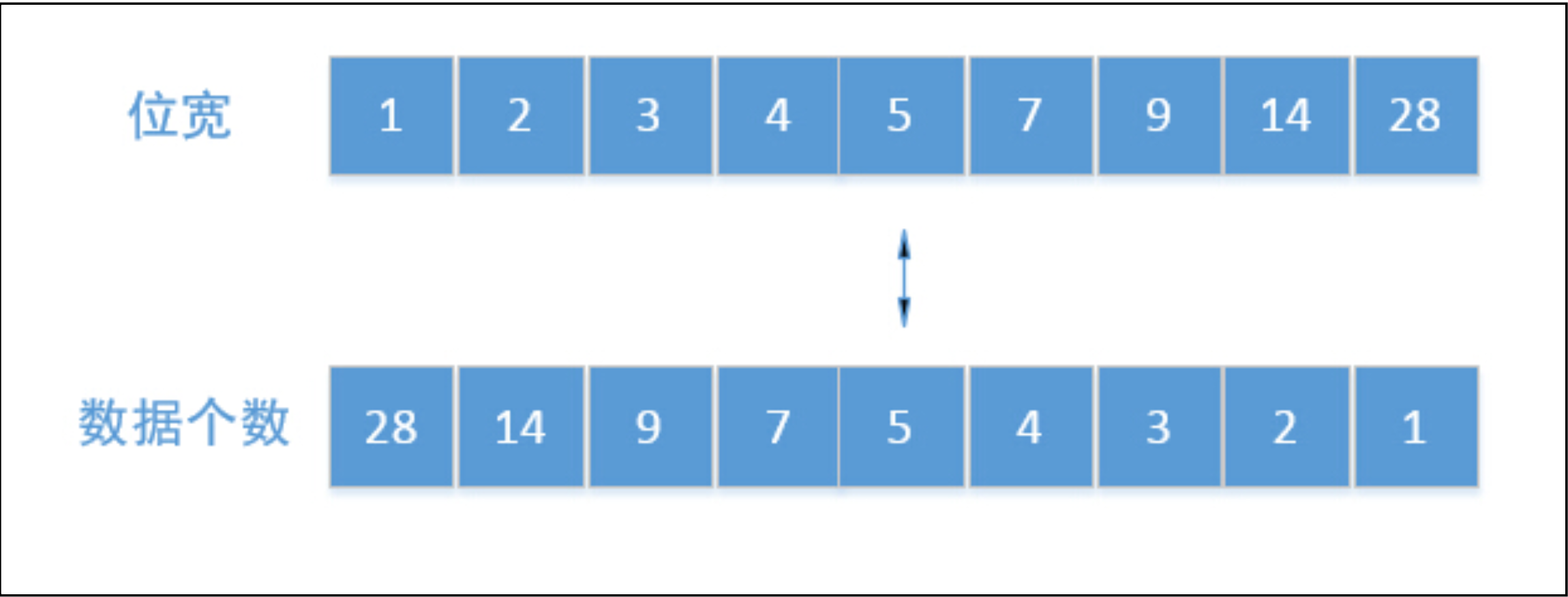
如上图所示，压缩后的数据，位宽有9种选择，分别为1、2、3、4、5、7、9、14、28，记为bits，那对应的压缩后的每个int数据(前4位为压缩模式)可以存储28、14、9、7、5、4、3、2、1，记为size。压缩的主要思路就是先查找合适的压缩位宽，之后再移位存储数据，详细流程为：

从首到尾依次遍历需要压缩的数据，按照上图可选择的位宽，从小到大遍历，可以获得位宽bits值和对应的能表示的数据个数size
设 i = 0，如果原始数据(src)小于位宽表示的最大值(1 << bits)，表示该bits能覆盖到此数据，则 i++，原始数据移动，直到位宽表示的最大值小于原始数据值跳出循环，此时能得到该位宽在原始数据中能覆盖的数据个数i的值
判断i是否与该位宽bits对应的size是否相等，如果相等，则表示该位宽bits能覆盖size个数据，得到该size个数可被压缩的位宽，然后原始数据移动size个数。如果i与此位宽bits对应的size不相等，则移动到下一个可选择的位宽，直到i与size相等为止

Simple 16

压缩方法

S16压缩算法，是Simple 系列压缩算法的一员，就是把一个32位的int类型分为两个区域，前四个bit记录后面28bit的使用方式，即模式，后面28位用来存放多个数值，只所以被称为S16，是因为前四个bit表示16种状态，与S9相比，更节省空间。列表如下:

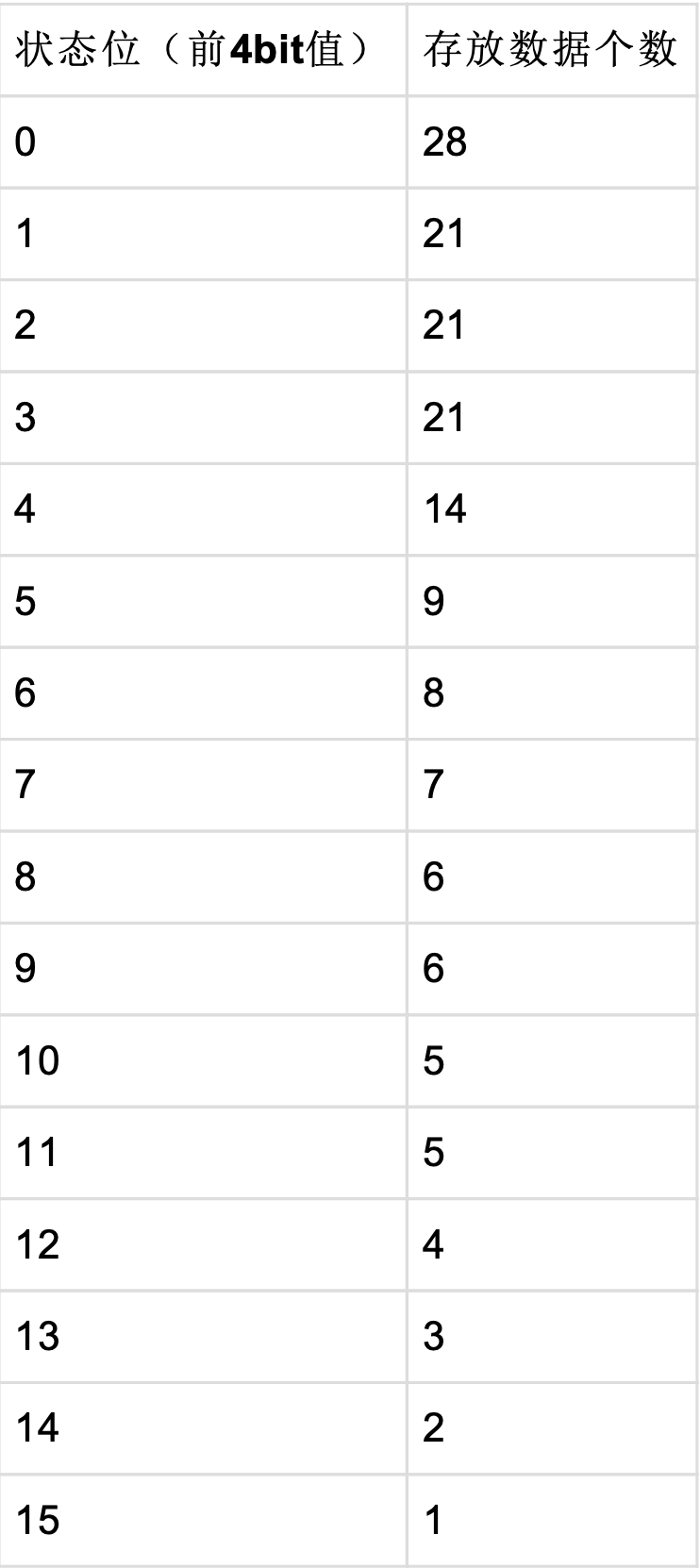
而每个数据占用的位数稍微有些复杂，代码里使用了一个以下二维数组进行表示，数组的每一行的每个值表示数值被压缩后的值，如bitCount数组所示。

const uint8_t S16Compressor::bitCount[16][28] = {
      {1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},
      {2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0},
      {1,1,1,1,1,1,1,2,2,2,2,2,2,2,1,1,1,1,1,1,1,0,0,0,0,0,0,0},
      {1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,0,0,0,0,0,0,0},
      {2,2,2,2,2,2,2,2,2,2,2,2,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
      {4,3,3,3,3,3,3,3,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
      {3,4,4,4,4,3,3,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
      {4,4,4,4,4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
      {5,5,5,5,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
      {4,4,5,5,5,5,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
      {6,6,6,5,5,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
      {5,5,6,6,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
      {7,7,7,7,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
      {10,9,9,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
      {14,14,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
      {28,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}
      };

压缩算法的实现与Simple 9 相似，这里不再详细介绍。

PForDelta

压缩方法

PForDelta 是一个专门用于倒排索引的压缩算法，用来解压缩DocList。DocList是存储文档的一个列表，以块为单位，一般每一个块(block)包含了128个文档，块里存储了文档的DocID，但是此id是以相邻文档DocID之间的差值表示的，所以，一般情况下此id值相对较小，使用sizeof(int)来表示一个整数，将大大的浪费了存储空间，所以可以使用选取较小的位宽来表示绝大部分这些数字id，即90%的数字可以用N为位宽来存储，称为normal值，剩余的10%值称为exception值，个数最大为12个 (128 * 10%)，然后每一个block头部再添加一个Header用来存储每一个block里的normal和exception信息。如下图所示，其为实现一个PForDelta算法需要的基础头信息：

isLastBlock占用1bit，表示是否为DocList里最后一个文档Block，如果为0，则表示不是最后一个Block，为1，则表示是最后一个Block
exceptionIntRange占用11bit，用来表示excetion数据被S9(Simple9压缩算法)压缩后的长度
frameBits占5bit，表示normal数据的最大位宽
firstExceptionPos占8bit，表示该Block块第一个exception值下标
dataNum占7bit，用来表示该Block里数据个数

PForDelta算法的核心就是找到正常值（可以用N位位宽存储）和异常值（小于12个数字），之后通过位移拼接成int。一个简单的示例如下：

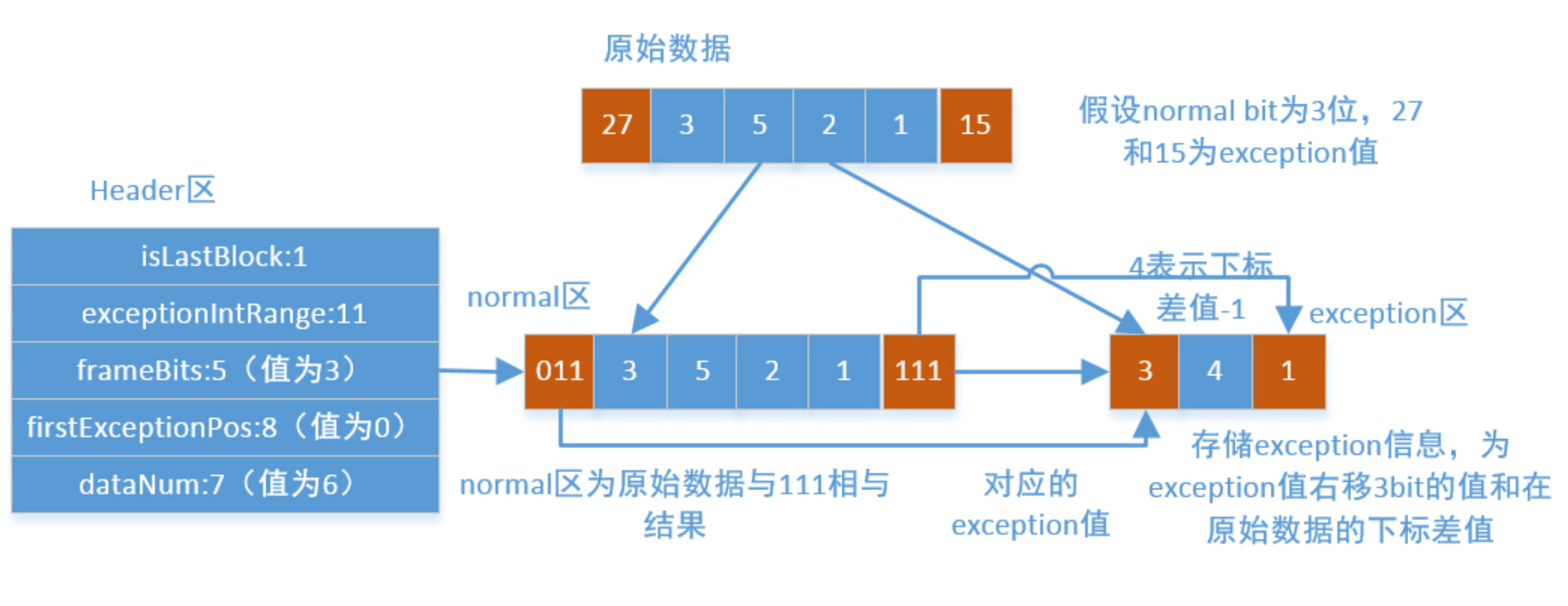
PForDelta算法解压时分为正常部分和异常部分的解压。正常部分只是将一系列按相同的bit位存储的数据顺序提取到数组中，即需要大量的位移操作，完全可以使用SIMD指令，所以很容易使用SIMD进行优化，详细可见：索引压缩算法New PForDelta简介以及使用SIMD技术的优化

Huffman Coding

压缩方法

哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是Huffman于1952年提出的一种编码方式，该方法完全依据字符出现概率进行构造的平均长度最短的编码，其采用最小冗余编码的算法进行压缩。其大致分为三步：

统计字符出现频率
根据频率构造一颗哈夫曼树，这也是一颗最优二叉树
对哈夫曼树进行01编码，得到最后的码文

详细可以查看动图霍夫曼编码算法：算法科普：有趣的霍夫曼编码

LZ77

压缩方法

LZ77算法是采用字典做数据压缩的算法。其核心思想：利用数据的重复结构信息来进行数据压缩。其方式就是把数据中一些可以组织成短语(最长字符)的字符加入字典，然后再有相同字符出现采用标记来代替字典中的短语，如此通过标记代替多数重复出现的方式以进行压缩。

LZ77的主要算法逻辑就是，先通过前向缓冲区预读数据，然后再向滑动窗口移入（滑动窗口有一定的长度），不断的寻找能与字典中短语匹配的最长短语，然后通过标记符标记。

目前从前向缓冲区中可以和滑动窗口中可以匹配的最长短语就是（A,B）,然后向前移动的时候再次遇到（A,B）的时候采用标记符代替。

压缩

当压缩数据的时候，前向缓冲区与移动窗口之间在做短语匹配的是后会存在2种情况:

找不到匹配时：将未匹配的符号编码成符号标记（多数都是字符本身）

找到匹配时：将其最长的匹配编码成短语标记。

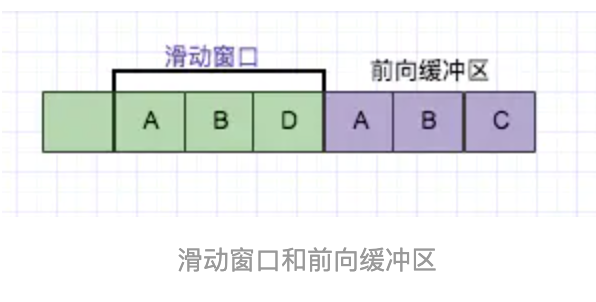
短语标记包含三部分信息：（滑动窗口中的偏移量（从匹配开始的地方计算）、匹配中的符号个数、匹配结束后的前向缓冲区中的第一个符号）。

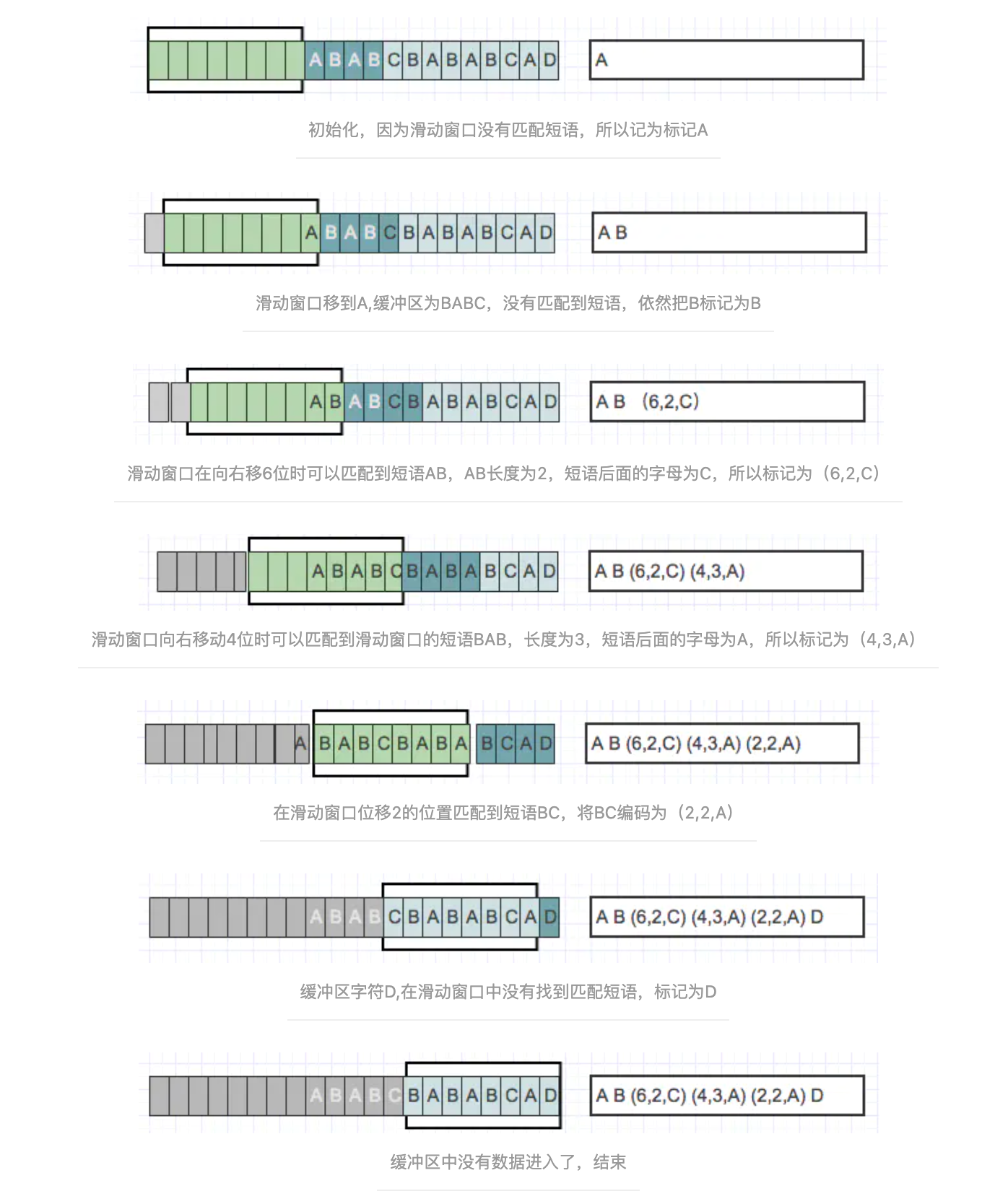
一旦把n个符号编码并生成响应的标记，就将这n个符号从滑动窗口的一端移出，并用前向缓冲区中同样数量的符号来代替它们，如此，滑动窗口中始终有最新的短语。通过图来进行解释：

Elasticsearch 行存压缩算法

上面简单介绍了霍夫曼和LZ77压缩算法，实际上很多压缩算法是其2种算法的变种或结合，ES默认有2种压缩算法，主要做行存(fdt)，分别是LZ4和DEFLATE，选择不同的压缩算法需要结合自己业务特点做tradeoff，比如这2种压缩算法的压缩比和性能对比如下：

索引配置best_compression相比配置default可以节省大约一半的磁盘空间，best_compression的压缩效果更好，写入或查询多消耗5%~9%的CPU。感兴趣的可以看下brotli和zstd压缩算法，据测试，codec-compression插件使用的brotli和zstd压缩算法，与默认压缩算法（LZ4）相比，写入性能下降了10%，压缩率提升了45%；与原生best_compression（DEFLATE）相比，写入性能不变，压缩率提升了8%。

参考链接：
图解LZ77压缩算法

前言

Fixed length

压缩方法

示例

Variable Byte

压缩方法

示例

Improved Variable Byte

压缩方法

示例

Group Varint

压缩方法

示例

Run Length Encoding

压缩方法

示例

Dictionary Coding

压缩方法

示例

Simple 9

压缩方法

Simple 16

压缩方法

PForDelta

压缩方法

Huffman Coding

压缩方法

LZ77

压缩方法

压缩

Elasticsearch 行存压缩算法

目录